This post is to memorize the reason why a system have all the poles with negative parts is stable.
Poles and Zeros
Poles and Zeros of a transfer function are the frequencies for which the value of the denominator and numerator of transfer function becomes zero respectively. The values of the poles and the zeros of a system determine whether the system is stable, and how well the system performs. Control systems, in the most simple sense, can be designed simply by assigning specific values to the poles and zeros of the system.
Physically realizable control systems must have a number of poles greater than or equal to the number of zeros. Systems that satisfy this relationship are called proper. We will elaborate on this below.
Time-Domain Relationships
Let’s say that we have a transfer function with 3 poles:
The poles are located at s = –l, –m, –n. Now, we can use partial fraction expansion to separate out the transfer function:
Using the inverse transform on each of these component fractions (looking up the transforms in our table), we get the following:
But, since s is a complex variable, l m and n can all potentially be complex numbers, with a real part (σ) and an imaginary part (jω). If we just look at the first term:
Using Euler’s Equation on the imaginary exponent, we get:
And taking the real part of this equation, we are left with our final result:
We can see from this equation that every pole will have an exponential part, and a sinusoidal part to its response. We can also go about constructing some rules:
- if σl = 0, the response of the pole is a perfect sinusoid (an oscillator)
- if ωl = 0, the response of the pole is a perfect exponential.
- if σl > 0, the exponential part of the response will decay towards zero.
- if σl < 0, the exponential part of the response will rise towards infinity.
From the last two rules, we can see that all poles of the system must have negative real parts, and therefore they must all have the form (s + l) for the system to be stable.

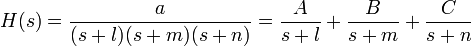


![Ae^{-\sigma_l t}[\cos(\omega_l t) - j\sin(\omega_l t)]u(t)](https://upload.wikimedia.org/math/2/2/6/2262d37015b6497a939062f08e3101c4.png)
